Quite the title, eh? It’s well known that the DA* 55mm f1.4 SDM lens is the successor to the FA* 85mm f1.4 lens. The difference is that the DA* 55mm lens is designed to take the crop factor into account to give the user an equivalent of 85mm on all current Pentax cameras.
So I was thinking today, why not compare the two lenses, but instead of a direct comparison, let’s consider things like crop factor (focal length multiplier), sensor size, and equivalence. What do we really lose with using lenses on crop sensors and how are things affected with additional tools like a teleconverter (TC). I don’t have a full-frame camera to test with, so I can only give you so much data here in regards to how crop factor affects output. I’m going to speculate and measure example photos to give you (and myself) a better understanding of what type of lens these two would be like if we had Equivalent full-frame lenses.
Equivalence is a touchy topic with some photographers. Some say it doesn’t exist, but I try to be a bit more practical in how I look at things. While the lens properties stay the same, there can be a noticeable difference in output given different factors.
The primary setup:
Pentax K-5 camera with a tripod. All of the photos were taken in full manual mode with exposure adjusted based on the meter in the camera. The FA* 85mm f1.4 lens was used alone and the DA* 55mm f1.4 lens was used with a Kenko Pz-AF 1.5x TELEPLUS SHQ teleconverter.
What equivalent full-frame lenses would these be like?:
FA* 85mm lens x 1.52 crop = 129.2 mm
Light usage for APS-C = 2x, f2.128
“It’s something like a 130mm f2 lens on full-frame.”
DA* 55mm lens x 1.52 crop = 83.6 x 1.5 TC = 125.4 mm
Light usage for APS-C with TC = 4x, f2.128 – 1 1/3 stop = f3.2
I decided on 1 1/3rd stop because it is a 1.5x TC and not 1.4 (1 stop) or 1.7 (1.5 stop).
“It’s something like a 125mm f3.2 lens on full-frame.”
In the case of the crop factor of 1.52, the lens aperture doesn’t actually change. The same goes for the focal length. The lens itself is exactly what it is regardless of the sensor behind it. The difference comes from how much light projected from the lens is used by the sensor.
Pretty confusing, isn’t it? Are our lenses really like a 130mm f2 and 125mm f3.2 on our APS-C camera? Well, let’s look into that a bit…
(85mm) Depth of field for the 130mm f2 calculation:
Subject distance = 50 ft
Depth of field = 5.38 ft
+4 stops (f8) = 22.5 ft
(55mm) Depth of field for the 125mm f3.2 calculation:
Subject distance = 50 ft
Depth of field = 9.29 ft
+4 stops (f10) = 32 ft
We know that a cropped sensor does lose out on a considerable amount of light these lenses could provide. We also know that given our calculations, these lenses should perform similarly with some difference in depth of field at a given aperture. The problem is we don’t have a full-frame camera to test out all aspects of equivalence, so we will just need to compare the two lenses together.
An image from each lens taken in manual exposure mode:
1/8000th, f1.4, ISO 100

While the settings and calculated focal length are essentially the same, we see that the 55mm lens is noticeably lower in exposure than the 85mm lens. Our calculation of f3.2 is making sense.
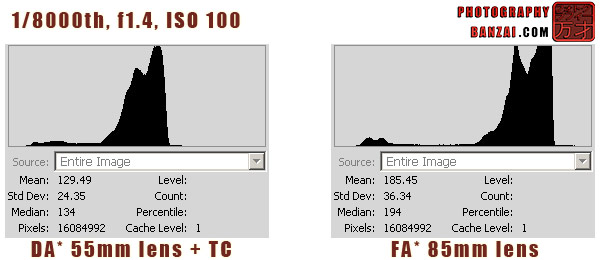
Histograms like these are showing the full red-green-blue color values in a 0-255 value graph. The left side is 0 (black) and the right is 255 (white). Often histograms are broken down into 10 equally spaced zones. In the zone system the 10 zones correspond to a stop of light each.
Our histograms go from 0-255, or 1-256. 256 / 10 = 25.6 pixels per zone.
If you look at the histograms above, you see that the mean (average) of the DA* 55mm image is 129.49 and the mean for the FA* 85mm is 185.45.
185.45 – 129.49 = 55.96 or 2.16 stops according to the zone system. That means our guess of f3.2 isn’t quite right as we expected 1 1/3rd stops. The DA* 55mm + TC according to this calculation would be closer to an f4 lens on full-frame. It’s possible I’m not interpreting all of the information or systems correctly, so take the values here with a grain of salt.
Let’s look at depth of field next:
Given that the DA* 55mm + TC combo has a smaller calculated aperture, that means the depth of field should be wider. This time I tried to properly expose each test image in the camera and I’ll also tweak them in Photoshop.

You can see that the 85mm lens has slightly more magnification, so our focal length calculation of 5mm difference looks correct. The background blur is significantly smoother on the 85mm lens. It looks like the focal point is off on one of the lenses, or it might just be the effects of limited depth of field at play. I also think the teleconverter is creating some odd distortion effects with the 55mm, but that’s not what we are focusing on here. According to our calculation above, at maximum aperture we should have about half the depth of field.
Let’s try a little harder and figuring out just how much more blur the 85mm lens produces. We know that there is a difference in focal length, so we should resize the image to match up.
The difference in calculated focal length of 129.2 mm – 125.4 mm = 3.8, means the DA* is 3.8 mm wider in field of view (FOV). Let’s try to take that into account with our next example. I resized the DA* 55mm’s image to match up the car’s features with the other image. This effectivly crops out the 5mm of extra FOV.

Blur spot (airy disk) size in pixels:

139 px / 177 px = 0.7853 * 100 = 78.5% difference.
From this website’s calculator, it gives us an airy disk sizes of 2.7um at f2 and 5.3um at f4 giving us around a 50% difference in that case. Using the value of f2.8 is 3.7um that gives us a value closer to 73%. So this seems to conflict with our exposure measurement in that histogram zone calculation makes the DA* 55mm + TC seem like a f4 lens, but the measurement of the airy disk makes it seem more like an f2.8 lens. Maybe the true equivalent is in the middle somewhere… say f3.2 from my initial estimation of aperture.
Given actual examples of photos and how they compare, the idea of equivalence has some merit in how you should go about using your tools. The 55mm lens has an aperture of f1.4, but with a teleconverter to make the lens around the same focal length as the 85mm, we see it just isn’t the same in properties like exposure and background blur. If Pentax does release a full-frame DSLR camera in the future and I’m able to get one, I’d like to update this article with the lenses attached in the same configuration to that camera. Until then we can only speculate if these lenses are equivalence to the calculated lens specifications in the beginning of this article.
I hope you found this article interesting. Just keep in mind I’m learning as I go and I can’t guarantee my calculations, or even the ideas on how things relate together. Half the fun is learning about the intricate details of photography and trying to better your understanding of how things work. That’s what I’m trying to do with an article like this. When you press the shutter, you will better know what to expect.
